概率与统计

大数定律

样本数量越多 算数平均值有越高的概率接近期望

算数平均值:

\[ \tilde{X} = \frac{x_1 + x_2 + \cdots + x_n}{n} \]

期望:

\[ E(X) = \mu \]

则

\[ 当n-> \infty, \tilde{X} -> \mu \]

中心极限定理

残差

• 真实值: \(y_i\)

• 预测值: \(\hat{y_i}\)

\[ \epsilon_i = y_i - \hat{y_i} \]

一阶统计量

期望

期望表示了随机变量可能取值的加权平均 权重是相应取值的概率

离散的随机变量X:

\[ \mathbb{E}(X) = \sum_{i}x_i P(X=x_i) \]

连续的随机变量X:

\[ \mathbb{E}(x) = \int_{-\infty}^{\infty}xPDF(x)dx \]

方差

方差度量了随机变量取值的离散程度 表示数据围绕期望的波动性

\[ Var(X) = \mathbb{E}[(X - \mathbb{E}(X))^2] = \mathbb{E}(X^2) - [\mathbb{E}(X)]^2 \]

离散型随机变量X:

\[ \sum_i(x_i - E(X))^2 P(X=x_i) \]

连续型随机变量X:

\[ \int_{-\infty}^{\infty}(x - \mathbb{E}(X))^2 PDF(x)dx \]

标准差

标准差是方差的平方根

\[ \sigma(X) = \sqrt{Var(X)} \]

二阶统计量

一阶统计量就是均值

\[ \mu = E[x] \]

二阶统计量描述均值之外的第二层结构

比如 方差 协方差 协方差矩阵

协方差

假设有两个随机变量X和Y 样本量为n 协方差定义为

\[ Cov(X,Y) = \frac{1}{n}\sum_{i=1}^{n}(X_i - \bar{X})(Y_i -\bar{Y}) \]

其中

• \(\bar{X}; \hat{Y}\)分别是X和Y的均值

• \((X_i - \bar{X})(Y_i - \bar{Y})\)表示每个样本的偏离量

协方差衡量两个变量一起变化的趋势

协方差矩阵

当有多维数据\(X \in \mathbb{R}^{n \times d}\)时

X的每一列为一个特征

则协方差矩阵\(C \in \mathbb{R}^{d \times d}\)定义为

注意 前提是X中心化了

\[ C = \frac{1}{n}X^T X \]

在协方差矩阵中

• 对角线\(C_{ii}\)表示第i个特征的方差(自己和自己的协方差)

• 非对角线\(C_{ij}\)表示第i个特征和第j个特征的协方差

PCC/Pearson

皮尔逊相关系数

PCC衡量两个变量之间线性关系的强度和方向

用于Lars回归等

\[ r_{xy} = \frac{Cov(X,Y)}{\sigma(X)\sigma(Y)} \]

PCC是对协方差进行标准化的结果 使得其范围在[-1,1]之间

• r=1:完美的正线性关系

• r=-1:完美的负线性关系

• r=0:几乎无线性关系

条件概率

在B事件发生的前提下 A事件发生的概率

\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)} \]

贝叶斯公式

在机器学习中的贝叶斯公式一般为

\[ P(C \mid X) = \frac{P(X \mid C)P(C)}{P(X)} \]

其中

• \(P(C \mid X)\): 给定输入X后 分类C发生的后验概率

• \(P(X \mid C)\): 在分类C下 输入X的似然(概率密度)(也就是PDF的y轴)

• \(P(C)\): 分类C的先验概率(训练数据集中该类别的出现频率)

• \(P(X)\): 输入X的总概率

似然

假设参数是w 这些数据有多合理

• 概率是 参数已知 问数据出现的可能性

• 似然是 数据已知 把它当作参数的函数

似然就是PDF曲线中的y值 而概率是PDF曲线的面积 注意这个不等于概率 似然不是概率分布 因为积分不一定为1

\mathcal{L}(\theta|y)

MAP

最大后验估计

在已经看到数据的前提下 选择后验概率最大的参数

\[ \hat{w}_{MAP} = \arg\max_{w} P(w \mid y) \]

因为P(y)与w无关: P(y)是把所有可能的w都积分的常数

所以MAP等效为

\[ \hat{w}_{MAP} = \arg\max_w P(y \mid w)P(w) \]

PDF

概率密度函数

概率密度函数是 描述连续型随机变量X取值分布 的函数

对于任意的PDF函数有:

• \(PDF(x) \geq 0\): 所有的概率>=0

• \(\int_{- \infty}^{\infty}PDF(x)dx = 1\): 所有的概率加起来=1

• \(P(a \leq X \leq b) = \int_{a}^{b}PDF(x)dx\): PDF底下的面积代表区间概率

PDF(x)也就是y值不直接表示概率 对于连续变量 单个点的概率严格为0(勒贝格测度)

高斯分布/正态分布

随机变量X服从正态分布表示为

\[ X \sim N(\mu,\sigma^2) \]

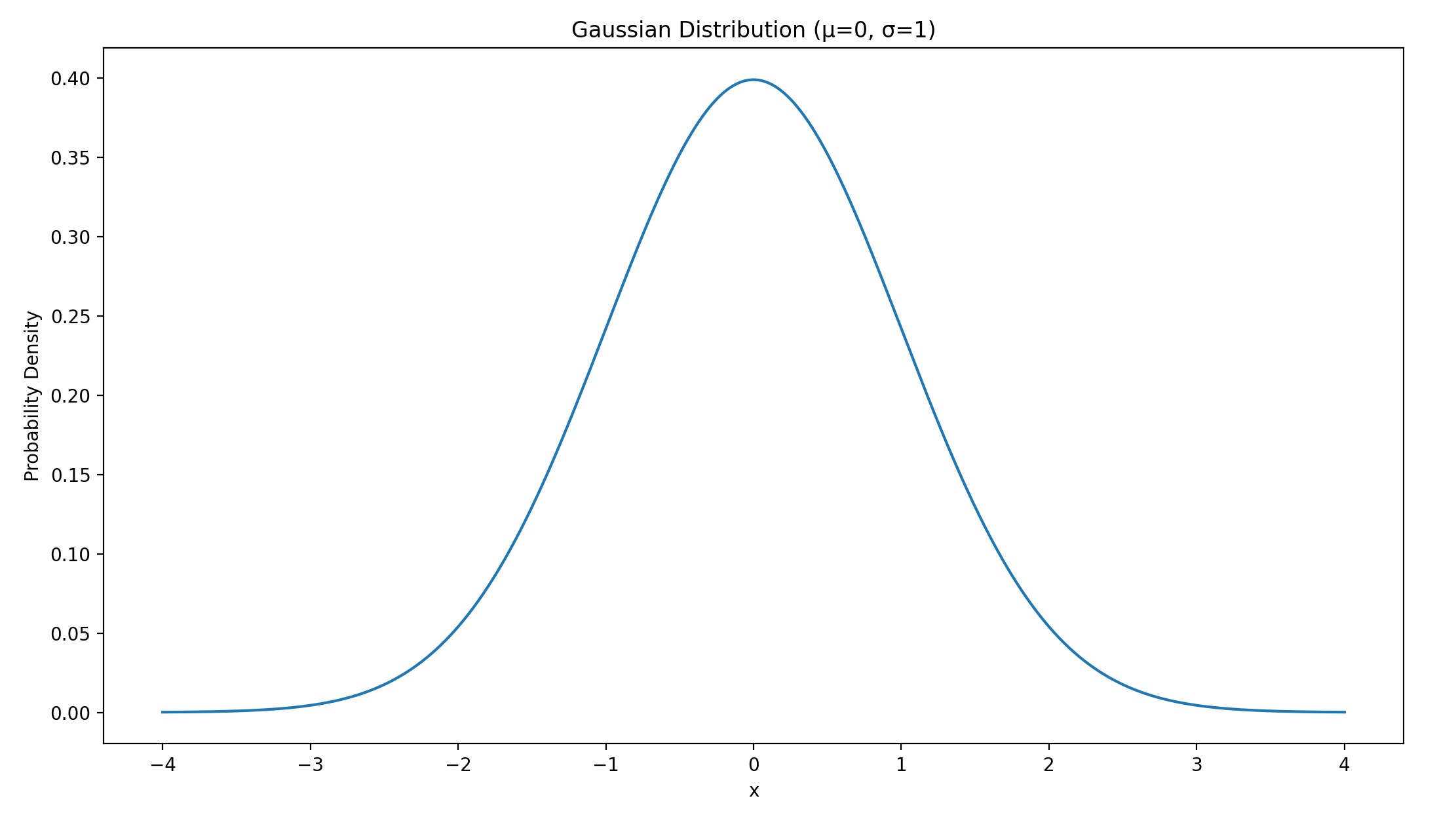
PDF:

\[ p(x) = \frac{1}{\sqrt{2 \pi \sigma^2} e^{-\frac{(x-\mu)^2}{2\sigma^2}}} \]

其中

• 最大值在\(x=\mu\)时

• 均值=众数=中位数

拉普拉斯分布

随机变量X服从拉普拉斯分布表示为

拉普拉斯先验的信念是 在深度学习中 参数本身是稀疏的

\[ X \sim Laplace(\mu,b) \]

PDF:

\[ p(x \mid \mu,b) = \frac{1}{2b} e^{(- \frac{|x - \mu|}{b})} \]

其中

• \(\mu\): 位置参数(中心)

• \(b\): 尺度参数

• 均值\(\mu\) 方差\(2b^2\) 中位数\(\mu\) 中枢\(\mu\)

PMF

概率